光時計をロケットの進行方向に沿って設置し, 光線をロケットの先端と後端を往復させ, ロケットの長さを測るとする.
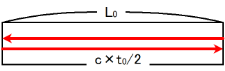
まずロケットに固定された $\text{K}_0$ 系において, ロケットの長さ $L_0$ は往復時間を $t_0$ とすると \[ L_0=\frac{ct_0}{2} \]
となる.
これを $K$ 系で見てみよう. 以下の $t$-$x$ グラフで分かるように, 光時計は運動しているために往路と復路で経過時間が異なる.
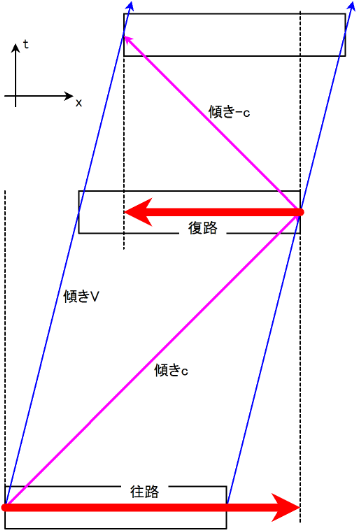
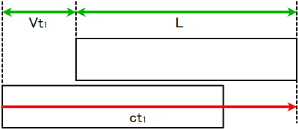
まず往路を計算しよう. $K$ 系におけるロケットの長さを $L$, 往路の経過時間を $t_1$ として \[ ct_1=L+Vt_1 \] これを $t_1$ について解けば \[ t_1=\frac{L}{c-V} \]
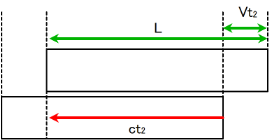
同様に復路の経過時間を $t_2$ とすれば \[ ct_2=L-Vt_2 \] なので, $t_2$ について解き \[ t_2=\frac{L}{c+V} \] こうして $K$ 系における光線の往復時間 $t=t_1+t_2$ は \[ t=\frac{2cL}{c^2-V^2} \] よってこれを $L$ について解けば \[ L=\frac{ct}{2}\left(1-\frac{V^2}{c^2}\right) \]
(1), (2) 及び $K_0$ 系と $K$ 系の間における時間の遅れの関係式 $t_0=\sqrt{1-\frac{V^2}{c^2}}t$ より \[ L-\sqrt{1-\frac{V^2}{c^2}}L_0 \] を得る.
$L_0$ は物体が静止しているときの長さであり, $L\leqq L_0$ なので, 運動物体の長さは静止時よりも縮んでいることが分かる.