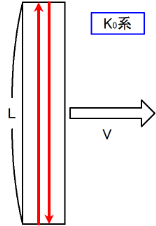
ロケット( $\text{K}_0$ 系)には, その進行方向と垂直な方向に往復する光時計が設置されている. 「光時計」とわざわざ名前が付いているが, 単に光線を往復させるだけのことである.
$\text{K}_0$ 系, $\text{K}$ 系ともに光の往復時間を求め, その違いを見てみよう. 尚, ロケットの床から天井までの長さを$\text{K}$ 系, $\text{K}_0$ 系共に変わらず $L$ であるとする. これは空間の線形独立性の現れであるのだが, この仮定で不整合な部分が生じれば修正すれば良いだけの事だ.
まずロケットに固定されている $\text{K}_0$ 系での光線の振る舞いを考えよう. 光線の往復時間 $t_0$ は \[ t_0=2Lc \] である. ($c$ は真空中の光速.)
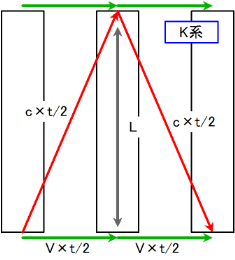
一方, 座標系 $\text{K}$ においては, 光線はロケット進行方向に傾いて進行していく. 三平方の定理を用いて \[ \left(c\times \frac{t}{2}\right)^2 = L^2+\left(V\times \frac{t}{2}\right)^2 \]
という式が成り立つ. これを $t$ について解けば \[ t=\frac{2L}{c\sqrt{1-\frac{V^2}{c^2}}} \]
を得る. (1), (2) を比較すれば, $K$ 系, $K_0$ 系それぞれにおける光線の往復時間 $t$, $t_0$ の関係は \[ t=\frac{t_0}{\sqrt{1-\frac{V^2}{c^2}}} \] となる事が分かる.
大小関係を見れば \[ t\geqq t_0 \] つまり $K_0$ 系では 1 秒間で起こる現象を $K$ 系で観測すると, それ以上の時間を掛けていることになる.