$\text{K}$ 系における座標を $x$, $t$, $K_0$ 系における座標を $x_0$, $t_0$ と表す.
前項より, $K_0$ 系における同時刻線 $t_0=0$ 上の点 $(x_0,\ 0)$ は, $\text{K}$ 系において直線 \[ t=\frac{V}{c^2}x \]
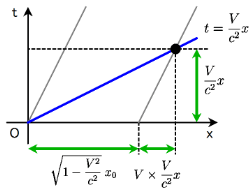
上にあることが分かった. 具体的に座標値を求めよう. $t=0$ のとき $x=\sqrt{1-V^2/c^2}x_0$ であった位置から, 速度 $V$ で時間 $\frac{V}{c^2}x$ の間だけ移動したことから \[ x=\sqrt{1-\frac{V^2}{c^2}}x_0+V\times\frac{V}{c^2}x \] これを $x$ について解くと \[ x=\frac{x_0}{\sqrt{1-\frac{V^2}{c^2}}} \] となるので, $K_0$ 系における座標 $(x_0,\ 0)$ は \[ (x,\ t)=\left(x,\ \frac{V}{c^2}x\right) =\left(\frac{x_0}{\sqrt{1-\frac{V^2}{c^2}}},\ \frac{\frac{V}{c^2}x_0}{\sqrt{1-\frac{V^2}{c^2}}}\right) \] となる.
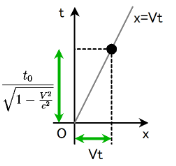
また, $K_0$ 系における固定された点 $x_0$ の座標 $(0,\ t_0)$ は $K$ 系では \[ (x,\ t)=(Vt,\ t) =\left( \frac{Vt_0}{\sqrt{1-\frac{V^2}{c^2}}},\ \frac{t_0}{\sqrt{1-\frac{V^2}{c^2}}} \right) \]
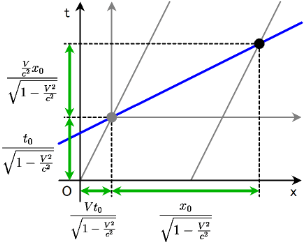
以上を合わせれば, $(x,\ t)$ は \[ (x,\ t)=\left(\frac{x_0+Vt_0}{\sqrt{1-\frac{V^2}{c^2}}},\ \frac{t_0+\frac{V}{c^2}x_0}{\sqrt{1-\frac{V^2}{c^2}}}\right) \]
こうして Lorentz 変換 \begin{align} x&=\frac{x_0+Vt_0}{\sqrt{1-\frac{V^2}{c^2}}}\notag \\ t&=\frac{t_0+\frac{V}{c^2}x_0}{\sqrt{1-\frac{V^2}{c^2}}}\notag \end{align} を得る.