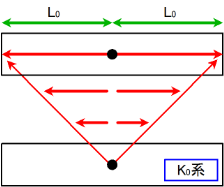
$\text{K}_0$ 系の原点からロケットの進行方向に沿って $-L_0$, $L_0$ の距離だけ離れた位置に測定器を設け, 原点から光線を放つ.
$\text{K}_0$ 系においては, 前後共に光線が同時に計測され, その経過時間は共に \[ \frac{L_0}{c} \] である.
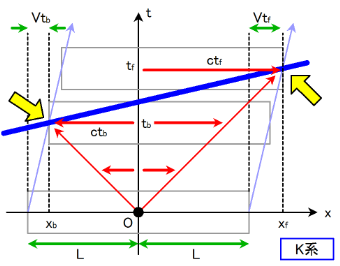
一方, $\text{K}$ 系においては後方が先に計測し, その後前方が計測する. 光線の放射した瞬間を座標の原点にとれば, 後方で計測されたときの位置及び時刻は \[ (x_b,t_b)=\left(-\frac{cL}{c+V},\ \frac{L}{c+V}\right) \] であり, 前方は \[ (x_f,t_f)=\left(\frac{cL}{c-V},\ \frac{L}{c-V}\right) \] である. ここで長さの縮み $L=\sqrt{1-V^2/c^2}L_0$ を考慮に入れている. これは $K_0$ 系において同時刻で起こった事象が, $K$ 系においては $t$-$x$ グラフで \[ \frac{t_f-t_b}{x_f-x_b}=\frac{\frac{L}{c-V}-\frac{L}{c+V}}{\frac{cL}{c-V}-\left(-\frac{cL}{c+V}\right)} =\frac{V}{c^2} \] という傾きを持っていることを意味する. 上の場合, 具体的には \[ t=\frac{V}{c^2}x+\frac{L}{c} \] が $\text{K}_0$ 系の同時刻線である.