セシウム137を毎日摂取したときの被曝線量率

結論

手っ取り早く知りたい人のために、どんな結論を得たのか予め示しておく。

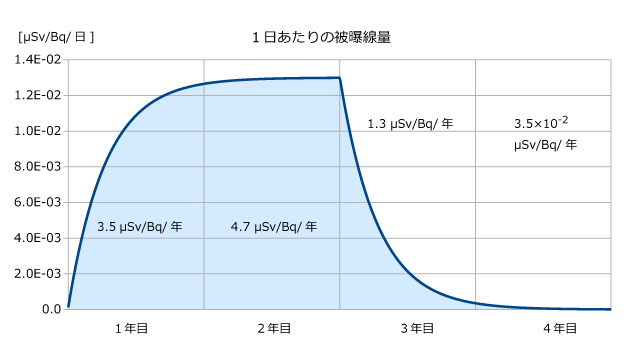
セシウム137を一定量、毎日２年間摂取し続けたとする。このときの被曝線量率は以下のようになる。

これは例えば毎日 10 Bq ずつ摂取し続けた場合、最初の年は 35 μSv で、２年目に 47 μSv、50年の累積で 95 μSv 被曝することを意味する。

預託実効線量

「日本の環境放射能と放射線」の「食品から受ける放射線量（預託実効線量）」によると

人体の組織に取り込まれた放射性物質は、その半減期および代謝による体外排出により、時間とともに減少します。

食品摂取後長期間にわたって人体が受ける内部被ばくの影響を評価する基準として、摂取後50年間に受ける線量を最初の１年で受けた（預託）として計算される「預託実効線量」が用いられます。

とある。(サイト [2] なども参照。) つまり摂取してから50年間の被曝量を累積しているので、以下の図の面積を求めていることになる。

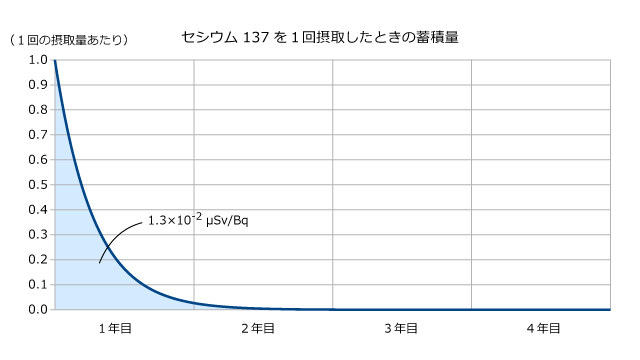
しかし、放射性物質を含む食品を毎日摂取し続けた場合、蓄積量は

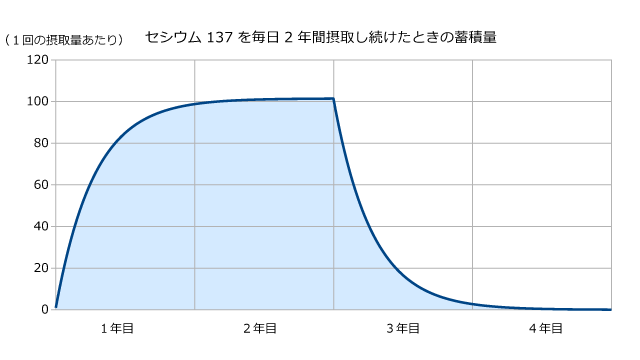
のような形になり[1]、連日の摂取を考慮する必要がある。

被曝量の計算

預託実効被曝線量

寿命 $\tau$、経過時間 $t$ とすると、連続摂取しない場合の被曝線量率の減衰は \[ e^{-t/\tau} \] に比例する。ここで寿命 $\tau$ と半減期 $T$ の間には \[ e^{-1/\tau} = \left(\frac{1}{2}\right)^{1/T} \] という関係がある。

摂取してから期間 $\sigma$ (=50年) の間の被曝線量 $E(\sigma)$ は、適当な係数 $k$ として \[ E(\sigma) = k\int_{0}^{\sigma}e^{-t/\tau}dt = k\tau (1-e^{-\sigma/\tau}) \]

１日の被曝線量

１日の被曝線量 $E$ は、 \[\begin{align*} E &= k\int_{0}^{1}e^{-t/\tau}dt = k\tau (1-e^{-1/\tau})\\ &= E(\sigma)\frac{1-e^{-1/\tau}}{1-e^{-\sigma/\tau}}\\ &= E(\sigma)\frac{1-\left(\frac{1}{2}\right)^{1/T}}{1-\left(\frac{1}{2}\right)^{\sigma/T}} \end{align*}\]

１日の摂取線量 $a$、初日を 0 日としたときの経過日数 $n$ の時の蓄積量 $S_n$ は \[ S_n = a\frac{1-\left(\frac{1}{2}\right)^{(n+1)/T}}{1-\left(\frac{1}{2}\right)^{1/T}} \] で与えられる[1]ので、実効線量係数を $\xi$ とすれば、経過日数 $n$ の預託実効線量 $E_n(\sigma)$ は \[ E_n(\sigma) = \xi S_n = a\xi\frac{1-\left(\frac{1}{2}\right)^{(n+1)/T}}{1-\left(\frac{1}{2}\right)^{1/T}} \] よって経過日数 $n$ における１日の被曝線量 $E_n$ \[ E_n = a\xi\frac{1-\left(\frac{1}{2}\right)^{(n+1)/T}}{1-\left(\frac{1}{2}\right)^{\sigma/T}} \] が得られる。

セシウム137の場合

文字に具体的な数値を代入していこう。$T$ = 70 [日]、$\sigma$ = 50 [年] = 1.8×10⁴ [日][3][4]、$\xi$ = 1.3×10^-5 [mSv/Bq][3][4]より \[ E_n / a = 1.3\times 10^{-2}\left\{1-\left(\frac{1}{2}\right)^{(n+1)/70}\right\}\ \ \text{[μSv/Bq/日]} \]

２年間毎日摂取する場合、$n$ は 0 から 729 までの値をとるので、 $E_n/a$ の値は \[ 1.3\times 10^{-4}\ \ \sim\ \ 1.3\times 10^{-2}\ \ \text{[μSv/Bq/日]} \]

年間被曝線量

１回の摂取量 $a$ あたりの１日被曝線量 $E_n/a$ は簡単な数列になっている。従って数列の和をとれば簡単に年間の被曝線量が求まる。

こうして初年と２年目の被曝線量率は

連続摂取がない場合の年間被曝線量

毎日２年間摂取し続けた後の年間被曝量も求めておこう。3年目以降をみるので、$Y$ を 365 [日] として、$n$ は $2Y$, $3Y$, $\cdots$ が入る。 \[\begin{align*} k\int_{n}^{n+Y} e^{-(t-2Y)/\tau} dt &= k\tau e^{-(n-2Y)/\tau}(1-e^{-Y/\tau}) \\ &= E(\sigma)e^{-(n-2Y)/\tau} \frac{1-e^{-Y/\tau}}{1-e^{-\sigma/\tau}} \\ &= E(\sigma)\left(\frac{1}{2}\right)^{(n-2Y)/T} \frac{1-\left(\frac{1}{2}\right)^{Y/T}}{1-\left(\frac{1}{2}\right)^{\sigma /T}} \end{align*}\]

$E(\sigma)$ は３年目から摂取しないため \[ E(\sigma) = a\xi\frac{1-\left(\frac{1}{2}\right)^{(2Y+1)/T}}{1-\left(\frac{1}{2}\right)^{1/T}} \] よって年間の被曝線量は以下のようになる。

従って、セシウム137を毎日２年間摂取し続けたときの50年被曝積算量は 9.5 μSv/Bq となる。

グラフ

冒頭にも見せたが、グラフにすると以下のようになる。

参考文献

• [1] 当サイト セシウム137を毎日摂取し続けたときの蓄積量
• [2] 緊急被ばく医療研修のホームページ 内部被ばくに関する線量換算係数
• [3] 専門家が答える暮らしの放射線Q&A 質問q-814
• [4] 専門家が答える暮らしの放射線Q&A 質問q-679