「Shizuoka+」の「【内部被曝】不検出レベルでも食べ続けると…」という記事。これは「放射線衛生研究」の記事を転載しているらしい。放射性セシウムが含まれる食品を食べるとどれくらい体内に蓄積していくのかをグラフ化している。
上記サイトではグラフのみが載っていて式がなかったので、当サイトで計算してみた。蓄積量は高校で学ぶ等比数列とその和で理解できる。
なお、ここでは蓄積量のみを求めたが、「セシウム137を毎日摂取し続けたときの被曝線量率」も求めたので続けて読んで欲しい。
注意:Internet Explorer 8 の場合、描画に時間がかかるので我慢すること。
数列の和を求めるために以下の記号を用いる。
| 文字 | 説明 |
|---|---|
| $n$ | 摂取回数 |
| $S_n$ | $n$ 回目の摂取の時点での放射性セシウム蓄積量 |
| $a$ | 1日の食事で摂取される放射性セシウムの量。等比数列の初項 |
| $r$ | 次の摂取までの放射性セシウム減衰率。等比数列の公比 |
さっそく求めていこう。$n$ 回目の摂取時の蓄積量 $S_n$ は、$n-1$ 回目の $S_{n-1}$ に $r$ を掛け、$a$ を足せばよい。
\[ \begin{align*} \text{1回目: } S_1 &= a \\ \text{2回目: } S_2 &= S_1 r + a\\ &= ar + a \\ \text{3回目: } S_3 &= S_2 r + a\\ &= ar^2+ar +a \\ &= a(1+r+r^2) \\ \hspace{-3em}\vdots & \hspace{2em}\vdots \\ \text{$n$回目: } S_n &= a(1+r+\cdots + r^{n-1}) \end{align*} \]
こうして蓄積量が等比数列の和の形で得られた。この和は
\[ \begin{align*} S_n &= a(1+r+\cdots + r^{n-1})\\ rS_n &= a(r+r^2+\cdots + r^{n-1} + r) \end{align*} \]
の両辺を引き算すれば簡単に求められ、最終的に \[ S_n = a\frac{1-r^n}{1-r} \] が得られる。
ちなみに、摂取と摂取の間における減衰はこの式には反映されないので注意。
仮に生涯ずっと定量摂取した場合、つまり $n\rightarrow\infty$ と極限をとろう。 \[ S_\infty = \frac{a}{1-r} \] これは放射性セシウムを仮に生涯ずっと定量摂取し続けたとしても、上限があることを意味する。
| 値 | |
|---|---|
| 物理的半減期 | 30.07年 [1] |
| 生物学的半減期 | 70日 [2] |
生物的半減期は「専門家が答える暮らしの放射線Q&A」 [2] によると
セシウムの生物学的半減期は、乳児で9日、9歳児で38日、30歳で70日、50歳で90日ですので、不安を長く抱え込む必要はありません。
とあるので、子供の方が短いことからとりあえず70日とした。
半減期の合成は、逆数の和で得られる。 \[ \frac{1}{\text{実効的な半減期}} = \frac{1}{\text{物理的半減期}} + \frac{1}{\text{生物学的半減期}} \]
物理的半減期を日数に直すと 30.07 × 365 = 10976 日 であり、生物学的半減期と比較すると無視できる値なので、実効的な半減期も70日としてしまってかまわない。(が、この後の計算では値をそのまま使って計算している...)
公比 $r$ は \[ r=\left(\frac{1}{2}\right)^{\text{日数}/\text{半減期70日}} \] なので、セシウム137を含む食品を摂取する頻度 $T$ (日) ごとの公比 $r$ は次の通りとなる。ついでに係数 $1/(1-r)$ も出しておこう。
| 頻度 $T$ | 公比 $r$ | $1/(1-r)$ |
|---|---|---|
| 1 | 0.99 | 100 |
| 7 | 0.93 | 15 |
| 14 | 0.87 | 7.7 |
| 30 | 0.74 | 3.9 |
| 60 | 0.55 | 2.2 |
上の表より、セシウム137を毎日 $a$ だけ摂取し続けると生涯で $100a$ 蓄積することになる。1週間おきだと $15a$、2週間おきだと $7.7a$、1ヶ月おきだと $3.9a$、2ヶ月おきだと $2.2a$ が体内に蓄積されることになる。
| 頻度 | 生涯の蓄積量 |
|---|---|
| 毎日 | 1日の100倍 |
| 1週間おき | 1日の15倍 |
| 2週間おき | 1日の7.7倍 |
| 1ヶ月おき | 1日の3.9倍 |
| 2ヶ月おき | 1日の2.2倍 |
計算をするときに $n\rightarrow\infty$ の極限をとったが、半減期と公比の値が得られたので、極限操作について評価しておこう。
$T=1$ のとき $r^n$ が 0.01 より小さくなる $n$ は 463 である。日数に換算すると 463 日で $r^n$ は 0.01 を下回る。 その他についても、462 + $T$ 日程度で生涯蓄積量に到達する事が分かる。
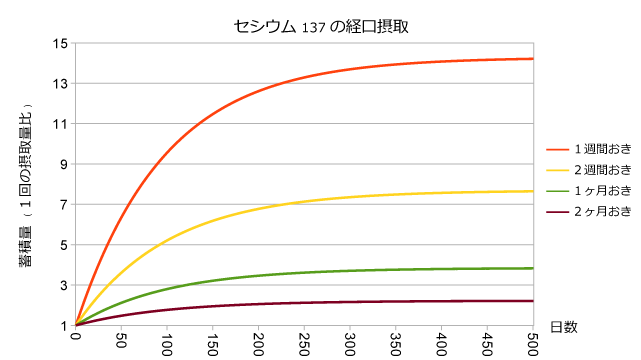
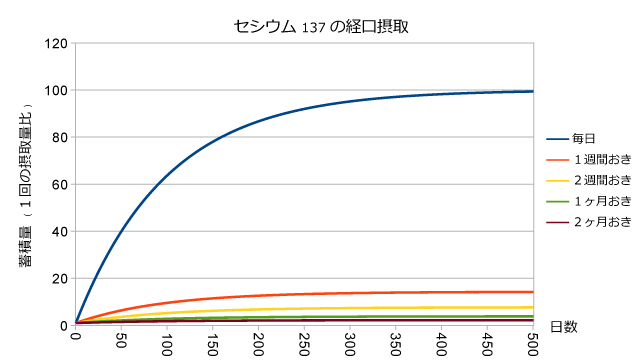
最初に出した蓄積量の式: \[ S_n = a\frac{1-r^n}{1-r} \] をグラフにしてみよう。$n$ は日付ではないので、 $n=(\text{日数}+T)/T$ として、初日(0日)から500日までのグラフを描いた。また、 $a$ によってグラフは変化するが、汎用的でないので $a$ を基準として何倍になるかというグラフにした。
繰り返しになるが、摂取と摂取の間における減衰は考慮していない。

毎日の摂取量だけが顕著なので、これを除いたのが以下のグラフ。