[何回買えば揃う？] < [自然科学] < [オレ研] < [TOP]

何回買えば揃う？

H15/02/04 (H16/10/29 改訂)

期待値

H15/02/04

ジュースのボトルキャップや、いわゆる食玩と呼ばれるオマケ付きお菓子にある、○○を集めよう！ というアレ。いったい何回買えば全て揃うのだろうか？

例えば、サイコロで５の目が出る為にはおよそ６回振ればいい。一般に、確率 P の事象であれば 1/P 回試行すればいいことになる。これを応用すればいいわけだ。

ランダムに当たる、n 種類のオマケを全て揃えたい。まず、１回買えば必ずどれかは手に入る。このオマケを A1 と名付けよう。次に、A1 以外のオマケを当てなければならないので、その確率は (n-1)/n である。従って n/(n-1) 回買えば A1 以外のオマケ A2 が当たることになる。

このようにして、A3 は n/(n-2) 回、A4 は n/(n-3) 回・・・と次々に買えば当たることが分かる。勿論、A3 とかの名前は「以前に当たったオマケ以外のうちのどれか」を意味し、特定のどれかではない。結局

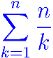
$\sum_{k=1}^{n}\frac{n}{k}$

を求めることになる。n の大きなところでは n*( γ + log(n) ) + 0.5 - 1/12n に近似できる[1]。γ= 0.57721... は Euler 定数である。

以下にオマケの種類が 2 から 20 までの場合における、平均的な必要購入回数を表にした。この回数を多いと見るか少ないと見るか・・・。ちなみに上に挙げた漸近形は 1/n で冪展開したものだが、非常に高い精度で一致している。

種類	期待値	漸近形
2	3.0000	2.9990
3	5.5000	5.4997
4	8.3333	8.3332
5	11.4167	11.4166
6	14.7000	14.6999
7	18.1500	18.1500
8	21.7429	21.7428
9	25.4607	25.4607
10	29.2897	29.2897
11	33.2187	33.2186
12	37.2385	37.2385
13	41.3417	41.3417
14	45.5219	45.5219
15	49.7734	49.7734
16	54.0917	54.0917
17	58.4724	58.4724
18	62.9119	62.9119
19	67.4071	67.4071
20	71.9548	71.9548

何回買えば揃う？補足の補足

H16/10/29

上の話の補足を書いたのだが、そこでは揺らぎの評価が間違っていた。独立試行における標準偏差は、各事象の分散の和のルートとなるのだが、補足ではルートの和をしてしまったのだ。それも粗い近似をした後で。そこでここではそれの正しい計算結果を紹介する。補足は自戒のために残しておく。

全分散は各分散 (1-p)/p^2 の和のルートで
n^2Σ1/k^2 - nΣ1/k　(和は k=1,2,・・・,n)
このルートが標準偏差となる。以下に期待値と標準偏差を載せておく。

種類	期待値	標準偏差
2	3.0000	1.4142
3	5.5000	2.5981
4	8.3333	3.8006
5	11.4167	5.0173
6	14.7000	6.2442
7	18.1500	7.4785
8	21.7429	8.7185
9	25.4607	9.9630
10	29.2897	11.2110
11	33.2187	12.4621
12	37.2385	13.7156
13	41.3417	14.9713
14	45.5219	16.2289
15	49.7734	17.4879
16	54.0917	18.7484
17	58.4724	20.0101
18	62.9119	21.2729
19	67.4071	22.5368
20	71.9548	23.8015

何回買えば揃う？補足

H15/02/17

上の話は飽くまでも期待値を評価しただけなので、それ程正確ではない。揺らぎがどれだけあるのかを気にしなければならないのである。

確率 p の事象が n 回目の試行で初めて起こる確率 P(n) は 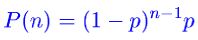$P(n)=(1-p)^{n-1}p$ で、従って期待値は 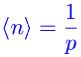<n>=1/p なわけだ。これを元にして計算したのが上の話。

さてこの確率の下で揺らぎを見てみると

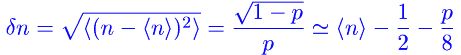
揺らぎの式

なので、期待値とほとんど同じ値であることがわかる。 p = 1 の場合は当然揺らぎはゼロである。そして今考えているケースは k を自然数として p=1/k という形なので、k が 2 以上のとき上の近似は正しい。だから確率 p の事象は 2/p 程度の回数をこなせばまず起こることになる。このことを考慮すれば、n 種類のオマケを全種類揃えるには期待値を 2 倍した

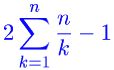
$2\sum_{k=1}^{n}\frac{n}{k}-1$

個程度買えばほぼ確実と言えるだろう。このようにして上の表は次のように修正される。

種類	揃うまでの平均購入回数	こんだけ買って揃わなかったら諦めろ
2	3	5
3	6	11
4	9	17
5	12	23
6	15	29
7	19	37
8	22	43
9	26	51
10	30	59
11	34	67
12	38	73
13	42	83
14	46	91
15	50	99
16	55	109
17	59	117
18	63	125
19	68	135
20	72	143

参考文献

分割数の漸近挙動

[コメントを書く]

[何回買えば揃う？] < [自然科学] < [オレ研] < [TOP]

種類	揃うまでの平均購入回数	こんだけ買って揃わなかったら諦めろ
2	3	5
3	6	11
4	9	17
5	12	23
6	15	29
7	19	37
8	22	43
9	26	51
10	30	59
11	34	67
12	38	73
13	42	83
14	46	91
15	50	99
16	55	109
17	59	117
18	63	125
19	68	135
20	72	143

種類	揃うまでの平均購入回数	こんだけ買って揃わなかったら諦めろ
2	3	5
3	6	11
4	9	17
5	12	23
6	15	29
7	19	37
8	22	43
9	26	51
10	30	59
11	34	67
12	38	73
13	42	83
14	46	91
15	50	99
16	55	109
17	59	117
18	63	125
19	68	135
20	72	143

何回買えば揃う？

期待値

何回買えば揃う？ 補足の補足

何回買えば揃う？ 補足

何回買えば揃う？補足の補足

何回買えば揃う？補足

種類	揃うまでの平均購入回数	こんだけ買って揃わなかったら諦めろ
2	3	5
3	6	11
4	9	17
5	12	23
6	15	29
7	19	37
8	22	43
9	26	51
10	30	59
11	34	67
12	38	73
13	42	83
14	46	91
15	50	99
16	55	109
17	59	117
18	63	125
19	68	135
20	72	143