放射性物質の個数の減衰を確率から求める

1体の場合

崩壊確率

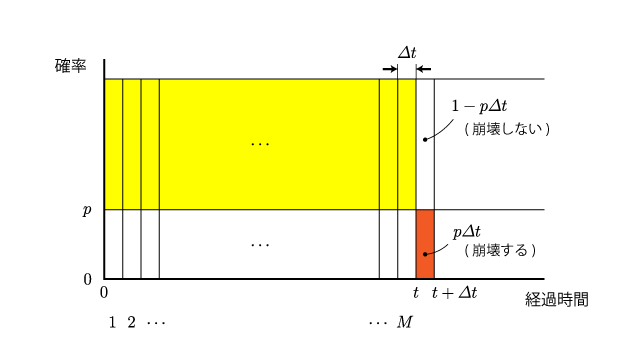
微小時間 $\varDelta t$ に放射性崩壊する確率を $p\varDelta t$ とする. $p$ は時間に依らない定数であり, 時間の逆数の次元を持っていることに注意しよう. 時間 $t$ だけ経ったときの, $t$ から $t+\varDelta t$ の間に崩壊する確率 $P(t)\varDelta t$ を求めよう. $t$ を $M$ 等分し, $\varDelta t=t/M$ として \begin{align} P(t)\varDelta t&=\lim_{M\to\infty}(1-p\varDelta t)^{M}p\varDelta t\label{eqn:one-body-naive-eq} \end{align}

と書ける. $(1-p\varDelta t)$ というのは, 時間間隔 $\varDelta t$ の間に崩壊しない確率である. $1$ から $M$ までが崩壊しないので $(1-p\varDelta t)$ の積(崩壊しない, かつ, 崩壊しない, かつ, $\cdots$ と $M$ 回繰り返し)があり, 最後に崩壊するので $p\varDelta t$ が掛かっている.

(1)式の両辺を $\varDelta t$ で割って整理すると \begin{align} P(t)&=\lim_{M\to\infty}\left(1-\frac{pt}{M}\right)^{M}p \end{align} と表せる. 極限はネイピア数(自然対数の底) $e$ の定義: \begin{equation} \lim_{M\to\infty}\left(1-\frac{pt}{M}\right)^{M}=e^{-pt} \end{equation} から, $P(t)$ は最終的に \begin{equation} P(t)=pe^{-pt}\label{eqn:Prob-one-particle-decay} \end{equation}

となる.

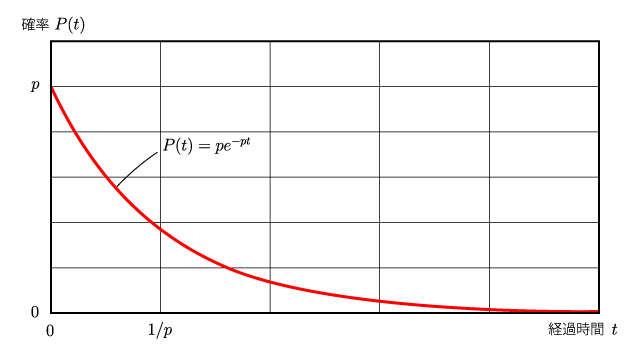
$P(t)$ は経過時間 $t$ を変数とする確率を表している. 事象の和は積分で与えられ, $0\leqq t\leqq\infty$ が区間である. 全確率が1であることを確認すると, 確かに \begin{equation} \int_{0}^{\infty}P(t)dt=\int_{0}^{\infty}pe^{-pt}dt =\int_{0}^{\infty}e^{-x}dx=1 \end{equation} となる.

繰り返しになるが(2)式を説明しよう. 瞬間瞬間の崩壊確率は一定の値 $p$ をとる. $P(t)$ は, $t=0$ からずっと崩壊せずにいて漸く $t$ で崩壊する確率である. 従ってその確率は時間経過と共に指数関数的に減少するのである.

寿命

崩壊確率はどの瞬間を切り取っても一定の値 $p$ である. 一方で, 特定の時間経過で崩壊する確率は $P(t)$ である. では実際に最も崩壊が起こり易いのはいつかというと, それは期待値を求めればよい. \begin{align} \int_{0}^{\infty}tP(t)dt&=\int_{0}^{\infty}pte^{-pt}dt\notag\\ &=\frac{1}{p}\int_{0}^{\infty}xe^{-x}dx\notag\\ &=\frac1p \end{align} つまり, 崩壊確率 $p$ のとき, 最も崩壊が起こりやすい経過時間はその逆数 $1/p$ であることが分かった. 粒子が崩壊するまでの時間 $1/p$ を寿命と呼ぶ.

寿命のゆらぎ

崩壊する時間の分散を計算し, ゆらぎを求めてみよう. \begin{align} \int_{0}^{\infty} t^2P(t)dt &=p^{-2}\int_{0}^{\infty}x^2e^{-x}dx\notag\\ &=\frac{2}{p^2} \end{align} よって \begin{align} \int_{0}^{\infty} t^2P(t)dt-\left(\int_{0}^{\infty} tP(t)dt\right)^2 &=\frac{1}{p^2} \end{align} したがって標準偏差は \begin{equation} \frac1p \end{equation} となり, 寿命と同じ時間だけゆらぎがあることが分かる.

N体の場合

崩壊する個数の確率

経過時間 $t$ に $N(t)$ 個あるとして, その中から微小時間 $\varDelta t$ の間に$n$個が崩壊する確率 $P_n(t)\varDelta t$ は \begin{align} P_n(t)\varDelta t&={}_{N}\text{C}_n (1-p\varDelta t)^{N-n}(p\varDelta t)^n\notag\\ &=\frac{N!}{n!(N-n)!}(1-p\varDelta t)^{N-n}(p\varDelta t)^n\label{eqn:prob-num-of-rad} \end{align} と表される. ここで ${}_{N}\text{C}_{n}$ は $N$ 個の中から $n$ 個を取り出す場合の数(コンビネーション, 組み合わせ)であり, 崩壊しない $N-n$ 個に関しては $(1-p\varDelta t)$ の積, 崩壊する $n$ 個に関しては $p\varDelta t$ の積となる. 確率を求めるときに時間間隔 $\varDelta t$ を考えるが, 確率自体に着目すると経過時間 $t$ は固定で崩壊数 $n$ が変数となっている. 区間は $0\leqq n \leqq N$ である.

さてここでも全確率が1であることを確かめておこう. (確率なんだから当然気になるはず!) \begin{align} \sum_{n=0}^{N}P_n(t)\varDelta t &=\sum_{n=0}^{N}\frac{N!}{n!(N-n)!}(1-p\varDelta t)^{N-n}(p\varDelta t)^{n}\notag\\ &=((1-p\varDelta t)+p\varDelta t)^{N}=1 \end{align} 2行目へは二項展開の公式を思いだそう. $P_n(t)\varDelta t$ は二項分布としてよく知られている確率分布である.

なお, 粒子数 $N$ が大きく崩壊確率 $p\varDelta t$ が小さいため, ポアッソン分布に近似することが出来るが, 詳細は省く.

崩壊数の期待値と微分方程式

崩壊数の期待値を求めよう. \begin{align} \sum_{n=0}^{N}nP_n(t)\varDelta t &=\sum_{n=0}^{N}n\cdot\frac{N!}{n!(N-n)!}(1-p\varDelta t)^{N-n}(p\varDelta t)^{n}\notag\\ &=\sum_{n=1}^{N}\frac{N!}{(n-1)!(N-n)!}(1-p\varDelta t)^{N-n}(p\varDelta t)^{n}\notag\\ &=\sum_{m=0}^{N-1}\frac{N!}{m!(N-m-1)!}(1-p\varDelta t)^{N-m-1}(p\varDelta t)^{m+1}\notag\\ &=Np\varDelta t\sum_{m=0}^{N-1}\frac{(N-1)!}{m!((N-1)-m)!}(1-p\varDelta t)^{(N-1)-m}(p\varDelta t)^{m}\notag\\ &=Np\varDelta t \end{align} "崩壊数の期待値"と書いたが, そもそも崩壊は確率的事象であるので, 右辺にある粒子数 $N(t)$ も本質的には期待値である. つまり崩壊数の期待値は粒子数 $N(t)$ の増分に負符号をつけた値に等しく, \begin{equation} -\varDelta N(t)=N(t) p\varDelta t \end{equation} これは $\varDelta t\to 0$ で微分方程式 \begin{align} \frac{dN(t)}{dt}&=-N(t)p \end{align} を得る. 我々が崩壊確率と呼んでいた $p$ は, 崩壊定数と呼ばれる量に等しいことが分かる. これを解いて, 粒子数の時間変化 \begin{align} N(t)&=N(0)e^{-pt}\label{eqn:num-of-particles} \end{align}

が得られる.

崩壊数のゆらぎ

崩壊する数の分散を計算し, ゆらぎを求めてみよう. \begin{align} \sum_{n=0}^{N}n^2P_n(t)\varDelta t &=\sum_{n=0}^{N}\frac{n^2N!}{n!(N-n)!}(1-p\varDelta t)^{N-m}(p\varDelta t)^n\notag\\ &=\sum_{n=1}^{N}\frac{nN!}{(n-1)!(N-n)!}(1-p\varDelta t)^{N-n}(p\varDelta t)^{n}\notag\\ &=\sum_{m=0}^{N-1}\frac{(m+1)N!}{m!(N-1-m)!}(1-p\varDelta t)^{N-1-m}(p\varDelta t)^{m+1}\notag\\ &=\sum_{l=0}^{N-2}\frac{N!}{l!(N-2-l)!}(1-p\varDelta t)^{N-2-l}(p\varDelta t)^{l+2}\notag\\ &\hspace{2em}+\sum_{m=0}^{N-1}\frac{N!}{m!(N-1-m)!}(1-p\varDelta t)^{N-1-m}(p\varDelta t)^{m+1}\notag\\ &=N(N-1)(p\varDelta t)^2+Np\varDelta t \end{align} よって分散は \begin{align} \sum_{n=0}^{N}n^2P_n(t)\varDelta t-\left(\sum_{n=0}^{N}nP_n(t)\varDelta t\right)^2 &=-Np^2\varDelta t^2+Np\varDelta t \end{align} となる.

従って, 時間 $t$ から $t+\varDelta t$ の間における崩壊数の標準偏差 $\sigma\varDelta t$ は \begin{equation} \sigma\varDelta t=\sqrt{Np\varDelta t(1-p\varDelta t)} \end{equation} であることが分かる. 粒子数の平方根に比例するため, 粒子数が大きくなるほどゆらぎの比は小さくなる.

半減期

(3)式に, 半減期 $t=T$, $N(t)=\frac12 N(0)$ を代入して \begin{align} \left(\frac12\right)^{1/T}&=e^{-p}\label{eqn:half-life} \end{align}

よって(3)式は \begin{equation} N(t)=N(0)\left(\frac12\right)^{t/T} \end{equation} とも書ける.

(4)式から寿命と半減期の関係は \begin{align} \frac1p&=\frac{T}{\log 2} \end{align} となる.